We want to make an object from a block of sturdy material like wood or metal by cutting material away. We have a router with a straight (square) bit. The design of the object may be complex. Perhaps we cannot produce all the features of the object faithfully with the given bit. Consider a drinking straw, for example. A router with a straight bit of diameter 9 mm cannot produce a straw of diameter 8 mm, as the tool is too wide to reach inside the straw without cutting the side of the straw.
Suppose the following conditions hold.
I developed a device to compute the volume of the resulting solid approximately. Here the device is applied to some simple designs. When the design is simple, we may compute the volume independently and compare our result to the output of the device. If our result is similar to that of the device, we will gain confidence in the accuracy of the device, and we will be inclined to trust the device when we apply it to more complex designs.
In the drawing below, the +x axis is red, the +y axis is green, and the +z axis is blue. The cutting tool plunges in the -z direction, that is, along the vector (x, y, z) = (0, 0, -1).
The cube is to be cut from a slightly larger block in the form of a cube 9 units by 9 units by 9 units. Expressed as a cartesian product of intervals of real numbers, the initial block is the set [1,10] x [1,10] x [1,10]. The object wanted after cutting is the 7 x 7 x 7 cube [2,9] x [2,9] x [2,9].
Q: How do we prevent the tool from cutting into the object? A: By surrounding the object with triangular facets. The triangulation shown below, for example, has a facet with vertices (2, 2, 9), (2, 9, 9), and (9, 9, 9); and a facet with vertices (2, 2, 9), (9, 2, 9), and (9, 9, 9). These two facets are enough to protect the cube when we cut from above only, as there is no undercutting, but for the sake of appearance, ten more facets cover the other five faces of the cube.
The legs of the triangles are drawn in black. The legs projected onto the xy plane are drawn in yellow, onto the xz plane in magenta, and onto the yz plane in cyan. The initial block is not shown, but the projections of its edges onto the three planes are drawn in brown.
We feed the design and the initial block into the device along with the bit radius (0.6 unit) and the cutting direction (0, 0, -1). Out comes the answer 390.9627. The design has volume 7 * 7 * 7 = 343, but the tool cannot reach the underside (that is, the -z side) of the object, so the remaining volume is actually 7 * 7 * 8 = 392. The estimate is off by less than 1%.
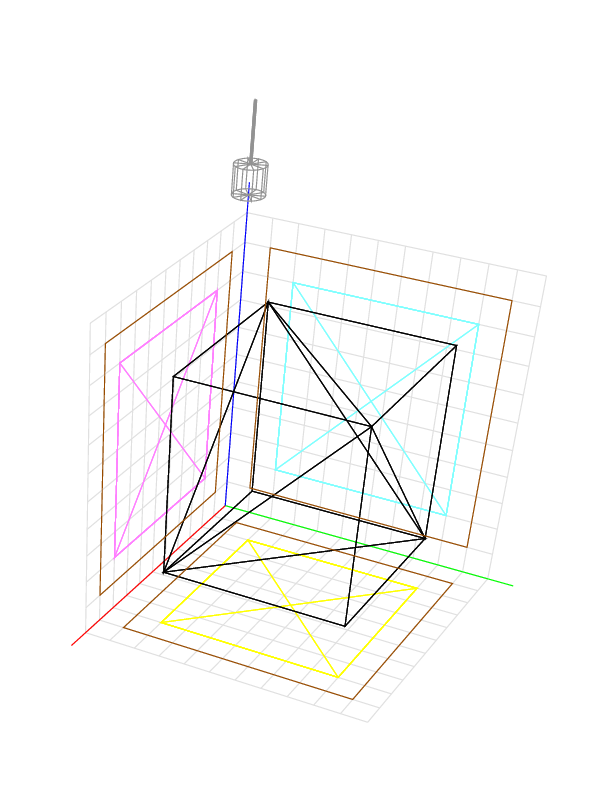
In order to reach the underside of the object, we may add another cutting direction. If we cut in directions (x, y, z) = (0, 0, -1) and (0, 0, 1), the estimate is 342.7758, again off by less than 1%.
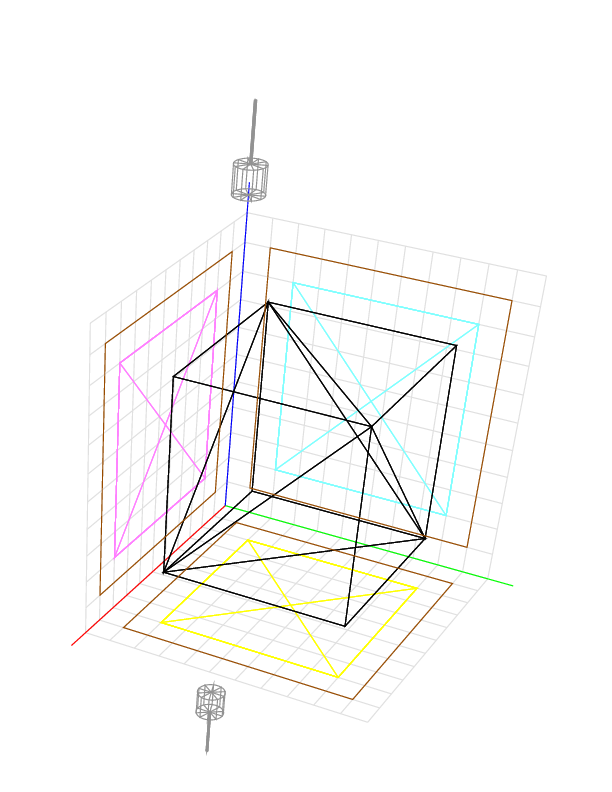
Another way to reach all sides of the object is to cut in directions (0, 0, -1) and (0, -1, 0). The device gives 343.7964.
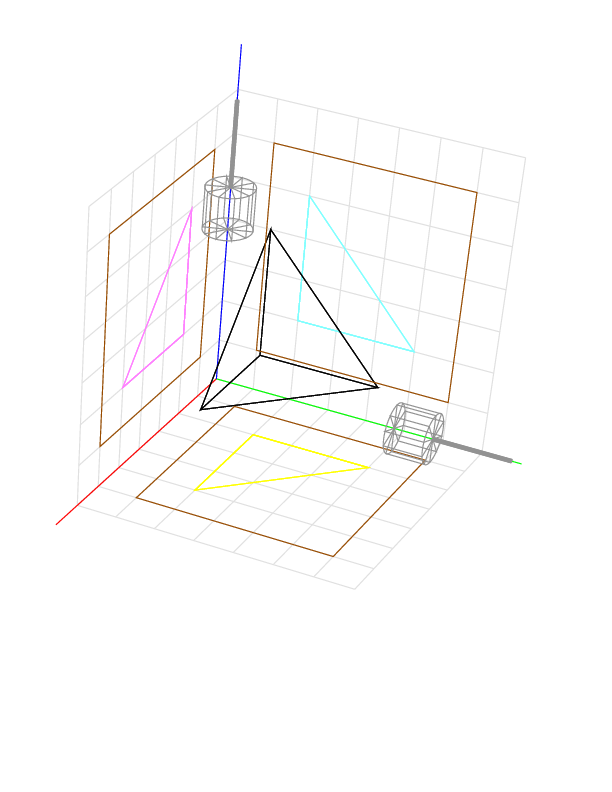
This example has a facet that is neither parallel nor perpendicular to the cutting directions. This tetrahedron has volume = base * height / 3 = (3 * 3 / 2) * 3 / 3 = 4.5, and the device gives 4.4625.
In this series, the object is like the cube [0,6] x [0,6] x [0,6] with a 2 x 2 square hole punched all the way through the middle from three directions, along the x axis, along the y axis, and along the z axis, so the three holes meet in the center of the cube. The volume of the object is 20 * 2 * 2 * 2 = 160. If we cut in direction (0, 0, -1) with a tiny (radius = 0.001) cutting bit that allows us to reach near the corners of the square holes, the remaining volume should be roughly 8 * 2 * 2 * 7 = 224, and the device gives 223.6928.
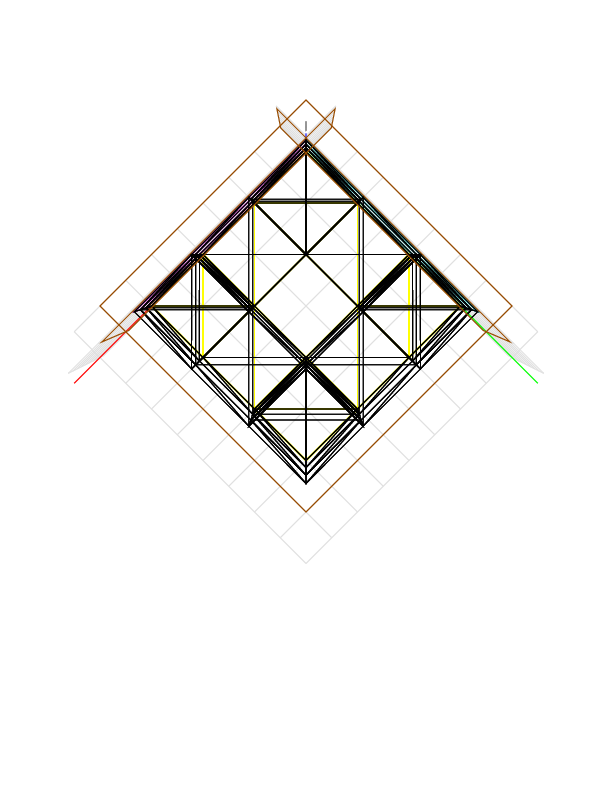
When the cutting bit is too large (radius = 1.1) to fit inside the hole, the volume remaining is 6 * 6 * 7 = 252, and the device gives 252.7744.
The object is the same as above. In the hollow cube, each of the three holes has length 6 and breadth 2 x 2, while the tool has radius 0.6. Cutting in the direction (0, 0, -1), the tool can enter the hole punched in the direction of the z axis, but the tool cannot reach all the material in the corners of the hole. After cutting, the remaining volume is 7 * (6 * 6 - 2 * 2 + (4 - pi) * 0.6 * 0.6) = 226.163, approximately. The device gives 222.6176, off by more than 1%. I ran it again another day and got 225.4848, 224.4608, and 223.8464.
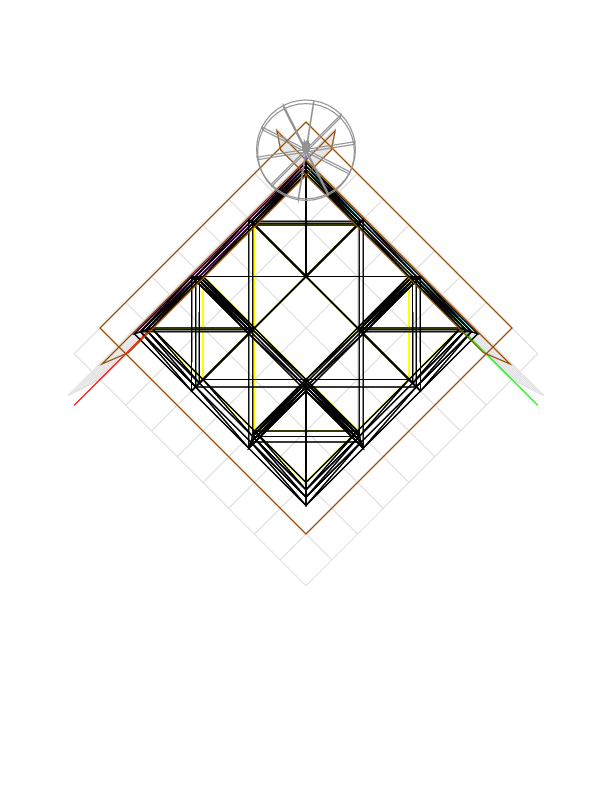
If we cut also in direction (0, -1, 0), the tool can reach through the hole parallel to the y axis. Each hole has volume 6 * (2 * 2 - (4 - pi) * 0.6 * 0.6) =~ 22.1458. The holes meet in the center of the cube. The volume of the intersection is 16 * 0.6 * 0.6 * 0.6 / 3 + (24 - 4 * pi) * 0.4 * 0.6 * 0.6 + 24 * 0.4 * 0.4 * 0.6 + 8 * 0.4 * 0.4 * 0.4 =~ 5.61444. After cutting, the volume remaining is approximately 6 * 6 * 6 - 2 * 22.1458 + 5.61444 =~ 177.323, and the device gives 175.9232.
We add one more cutting direction to reach the rest of the material. The device gives 165.2224.

This cup is a polyhedral approximation of a cylindrical cup with outer radius 4 units, inner radius 3, and height 11. The sides and bottom are 1 unit thick. Cutting from below, the tool cannot reach inside the cup. The blank extends 2 units above (and below) the cup top, so the volume remaining is roughly 13 * pi * 4 * 4 =~ 653.451. More precisely, the side of the cup is not really round, but has 21 flat faces. The true volume remaining is 13 * 21 * 4 * sin(pi/21) * 4 * cos(pi/21) =~ 643.745. The device gives 638.43.
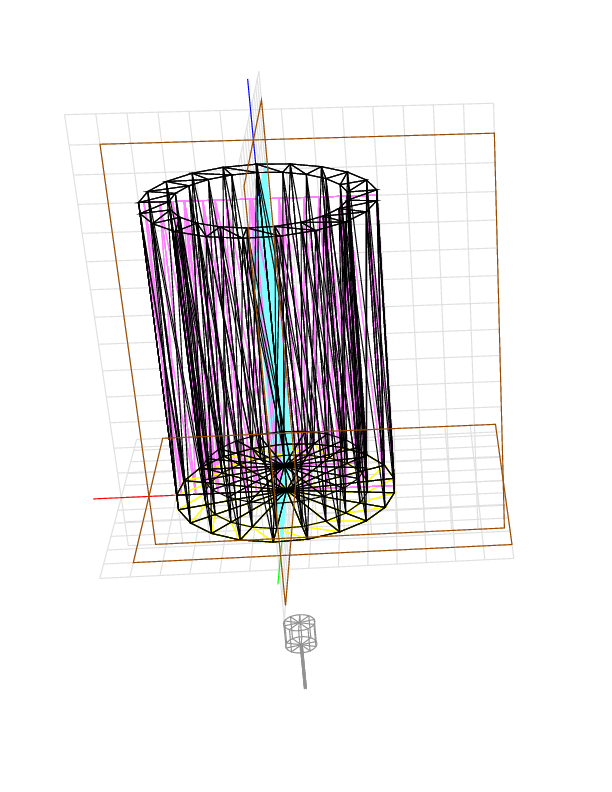
If instead we cut from above, the volume remaining is roughly 13 * pi * 4 * 4 - 10 * pi * 3 * 3 =~ 370.708, or more precisely, 13 * 21 * 4 * sin(pi/21) * 4 * cos(pi/21) - 10 * 21 * 3 * sin(pi/21) * 3 * cos(pi/21) =~ 365.202. The device gives 363.675 .
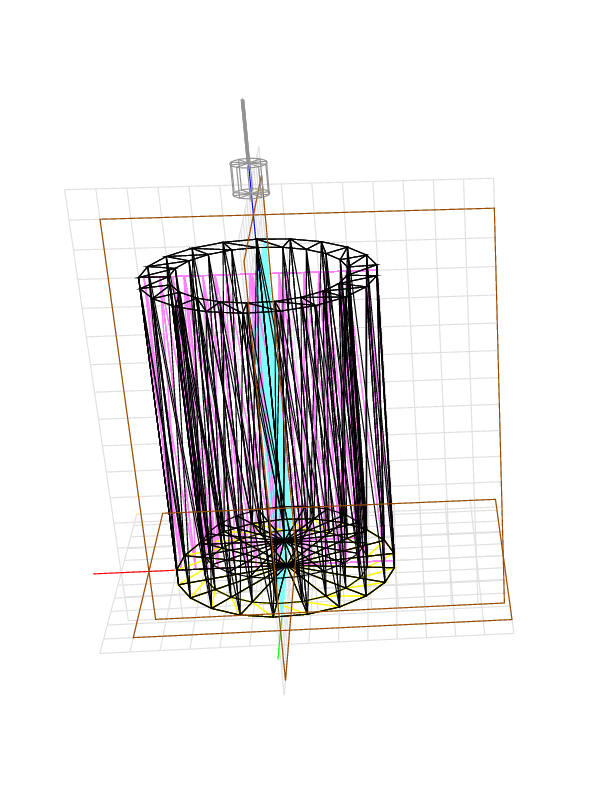
If we cut from both above and below, the volume remaining is roughly 11 * pi * 4 * 4 - 10 * pi * 3 * 3 =~ 270.177, or more precisely, 11 * 21 * 4 * sin(pi/21) * 4 * cos(pi/21) - 10 * 21 * 3 * sin(pi/21) * 3 * cos(pi/21) =~ 266.164. The device gives 278.46. On another day I got 260.52 and 271.83. The device runs on electricity. Right now it is configured to use little power. It will produce more accurate results if we turn up the power.
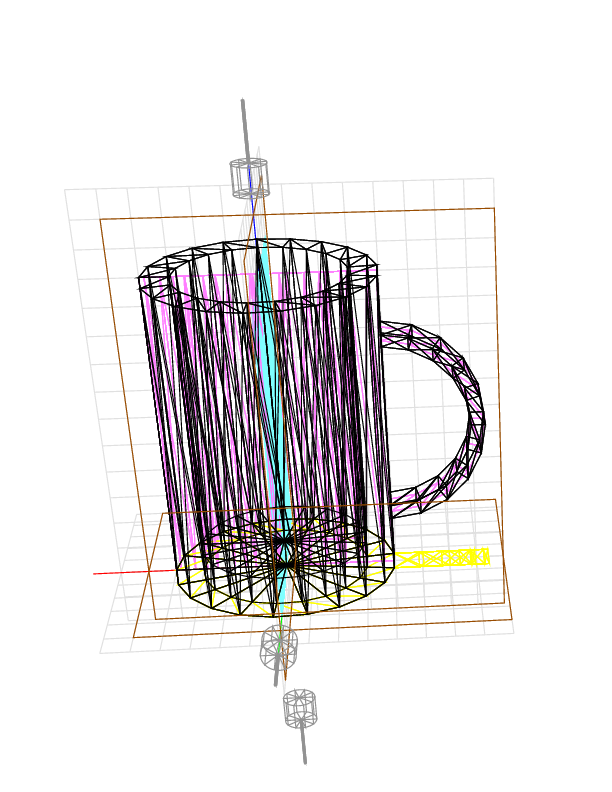
A handle is added to the cup. The device gives 692.64.

The device gives 415.74.

The device gives 285.675.
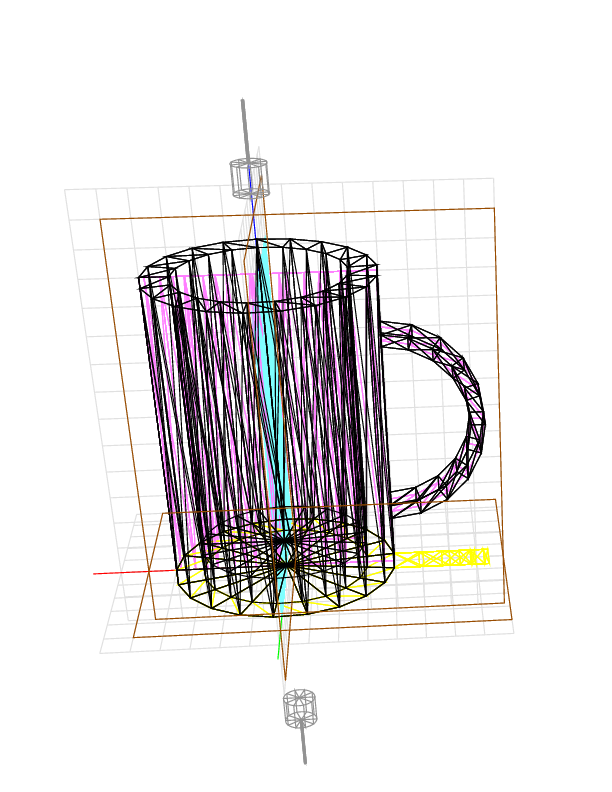
If we cut also in the y direction, we remove most of the material between the handle and the mug. The device gives 269.1.
|
Thank you for reading this technical note. My aim is to help people in industry with scheduling and estimating costs. No promises, but if you send me a small design, say of at most 5000 triangles and at most 7 cutting directions, I will run the device on your design and send you the result. Please include all the parameters described above. Email me at david.a.c.v.smith@gmail.com with subject VOLUME. If you send an STL file, I will find it easier to read text (ASCII) rather than binary. I can accept .zip files or files compressed in the style of Unix (https://kb.iu.edu/d/aeqx).