Question

We want to make an object from a block of sturdy material like wood or metal by cutting material away. We have a router with a straight (square) bit. The design of the object may be complex. Perhaps we cannot produce all the features of the object faithfully with the given bit. Consider a drinking straw, for example. A router with a straight bit of diameter 9 mm cannot produce a straw of diameter 8 mm, as the tool is too wide to reach inside the straw without cutting the side of the straw.

Suppose the following conditions hold.

1. The design of the object is expressed as a collection of triangular facets in 3-dimensional space. Each facet is the convex hull of its three vertices, where each vertex is a triple of real numbers.
2. The cutting tool consists of twin square blades at the end of a spindle. When the tool spins, it makes a cylinder-shaped hole.
3. Our only concern is to remove as much material as we can without allowing the tool to pass through a facet.
4. The tool may move around in space in three directions (x, y, z) by translation. It would be convenient also to rotate the tool in order to approach the block from various directions. However, it is a constraint of the equipment that the axis of the spindle cannot be rotated except by a time-consuming intervention. The tool has an automatic operating system that
   • reads the design file,
   • knows the diameter of the cutting tool and the orientation of the spindle, and
   • moves the cutting tool in directions x, y, and z.
5. There is no undercutting. All cuts are made as if the tool plunged toward the block along the axis of its spindle.

An answer

I developed a device to compute the volume of the resulting solid approximately. Here the device is applied to some simple designs. When the design is simple, we may compute the volume independently and compare our result to the output of the device. If our result is similar to that of the device, we will gain confidence in the accuracy of the device, and we will be inclined to trust the device when we apply it to more complex designs.

Cube cut from above

In the drawing below, the +x axis is red, the +y axis is green, and the +z axis is blue. The cutting tool plunges in the -z direction, that is, along the vector (x, y, z) = (0, 0, -1).

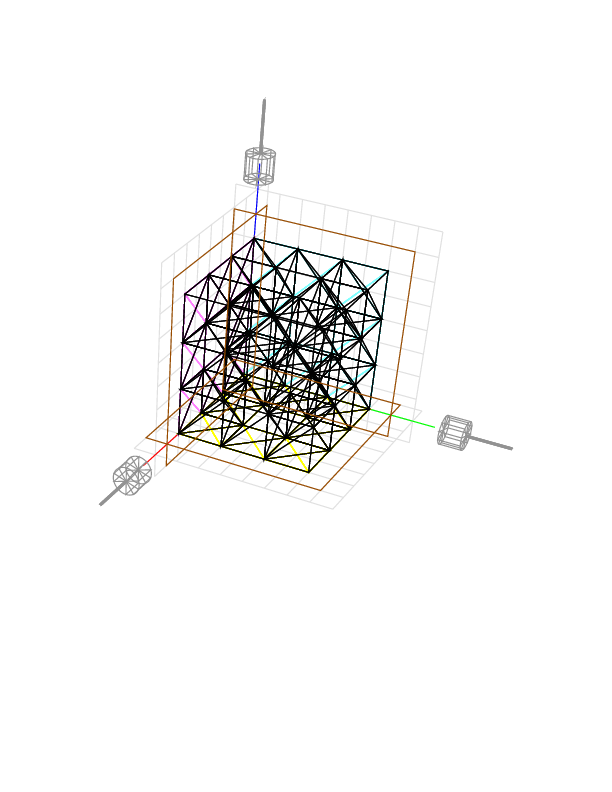
The cube is to be cut from a slightly larger block in the form of a cube 9 units by 9 units by 9 units. Expressed as a cartesian product of intervals of real numbers, the initial block is the set [1,10] x [1,10] x [1,10]. The object wanted after cutting is the 7 x 7 x 7 cube [2,9] x [2,9] x [2,9].

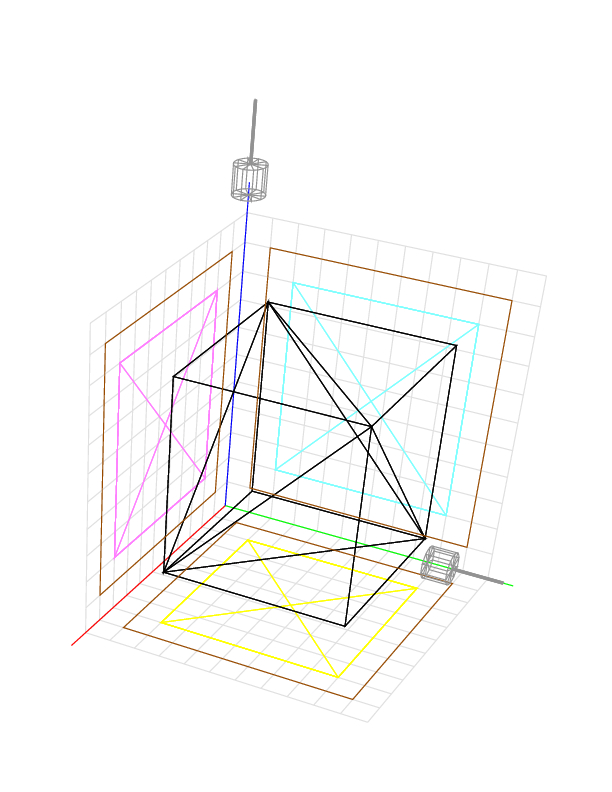
Q: How do we prevent the tool from cutting into the object? A: By surrounding the object with triangular facets. The triangulation shown below, for example, has a facet with vertices (2, 2, 9), (2, 9, 9), and (9, 9, 9); and a facet with vertices (2, 2, 9), (9, 2, 9), and (9, 9, 9). These two facets are enough to protect the cube when we cut from above only, as there is no undercutting, but for the sake of appearance, ten more facets cover the other five faces of the cube.

The legs of the triangles are drawn in black. The legs projected onto the xy plane are drawn in yellow, onto the xz plane in magenta, and onto the yz plane in cyan. The initial block is not shown, but the projections of its edges onto the three planes are drawn in brown.

We feed the design and the initial block into the device along with the bit radius (0.6 unit) and the cutting direction (0, 0, -1). Out comes the answer 390.9627. The design has volume 7 * 7 * 7 = 343, but the tool cannot reach the underside (that is, the -z side) of the object, so the remaining volume is actually 7 * 7 * 8 = 392. The estimate is off by less than 1%.

Cube cut from above and below

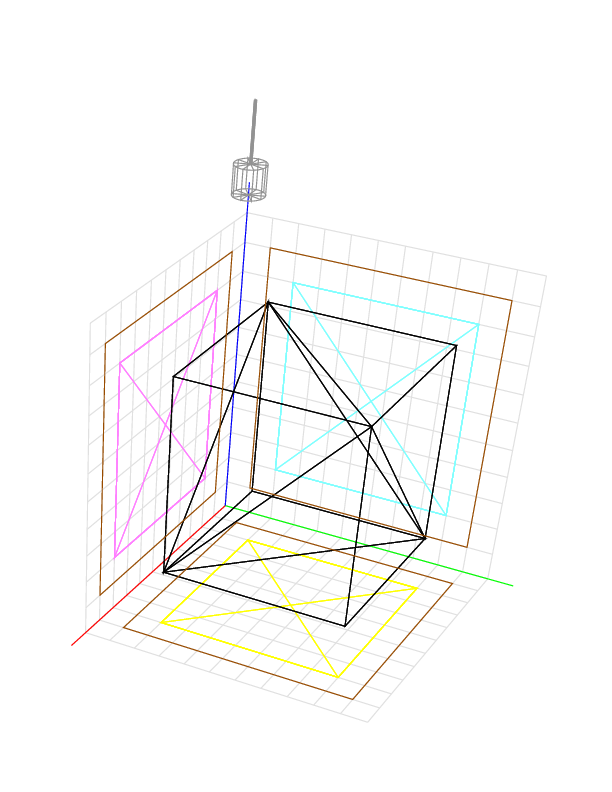
In order to reach the underside of the object, we may add another cutting direction. If we cut in directions (x, y, z) = (0, 0, -1) and (0, 0, 1), the estimate is 342.7758, again off by less than 1%.

Cube cut from above and from one side

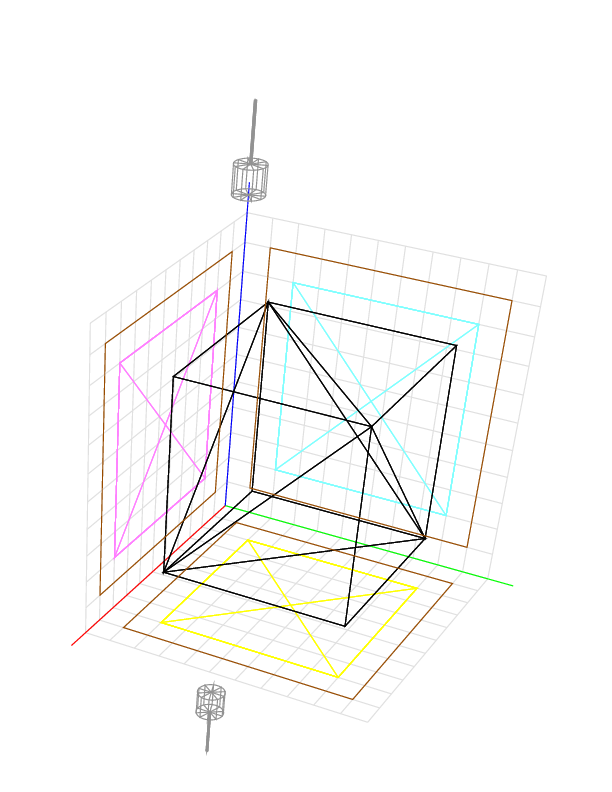
Another way to reach all sides of the object is to cut in directions (0, 0, -1) and (0, -1, 0). The device gives 343.7964.

Tetrahedron cut from above and from one side

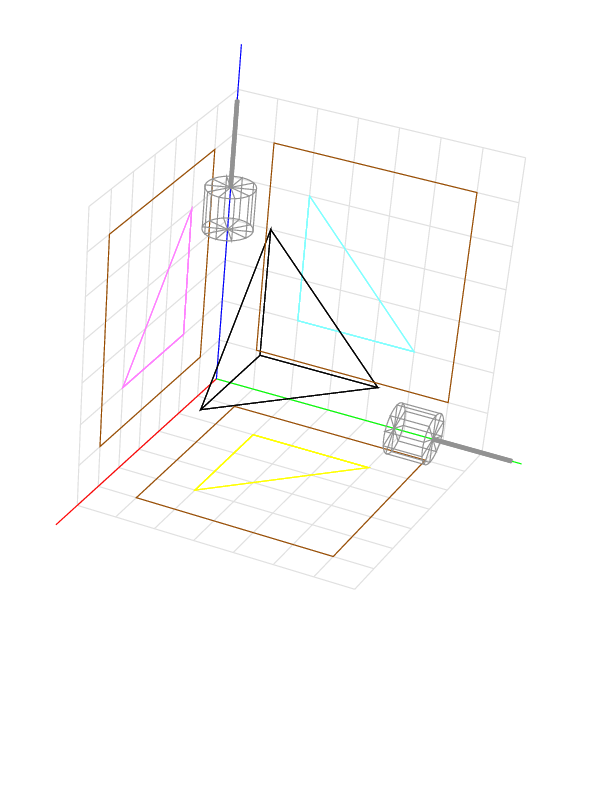
This example has a facet that is neither parallel nor perpendicular to the cutting directions. This tetrahedron has volume = base * height / 3 = (3 * 3 / 2) * 3 / 3 = 4.5, and the device gives 4.4625.

Hollow cube cut from above by tiny cutting tool

In this series, the object is like the cube [0,6] x [0,6] x [0,6] with a 2 x 2 square hole punched all the way through the middle from three directions, along the x axis, along the y axis, and along the z axis, so the three holes meet in the center of the cube. The volume of the object is 20 * 2 * 2 * 2 = 160. If we cut in direction (0, 0, -1) with a tiny (radius = 0.001) cutting bit that allows us to reach near the corners of the square holes, the remaining volume should be roughly 8 * 2 * 2 * 7 = 224, and the device gives 223.6928.

Hollow cube cut from above by huge cutting tool

When the cutting bit is too large (radius = 1.1) to fit inside the hole, the volume remaining is 6 * 6 * 7 = 252, and the device gives 252.7744.

Hollow cube cut from above

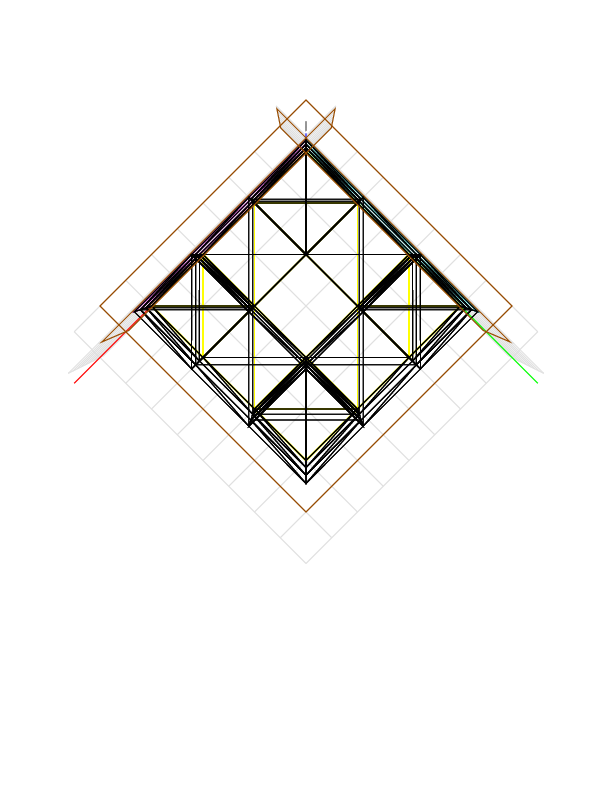
The object is the same as above. In the hollow cube, each of the three holes has length 6 and breadth 2 x 2, while the tool has radius 0.6. Cutting in the direction (0, 0, -1), the tool can enter the hole punched in the direction of the z axis, but the tool cannot reach all the material in the corners of the hole. After cutting, the remaining volume is 7 * (6 * 6 - 2 * 2 + (4 - pi) * 0.6 * 0.6) = 226.163, approximately. The device gives 222.6176, off by more than 1%. I ran it again another day and got 225.4848, 224.4608, and 223.8464.

Hollow cube cut from above and from one side

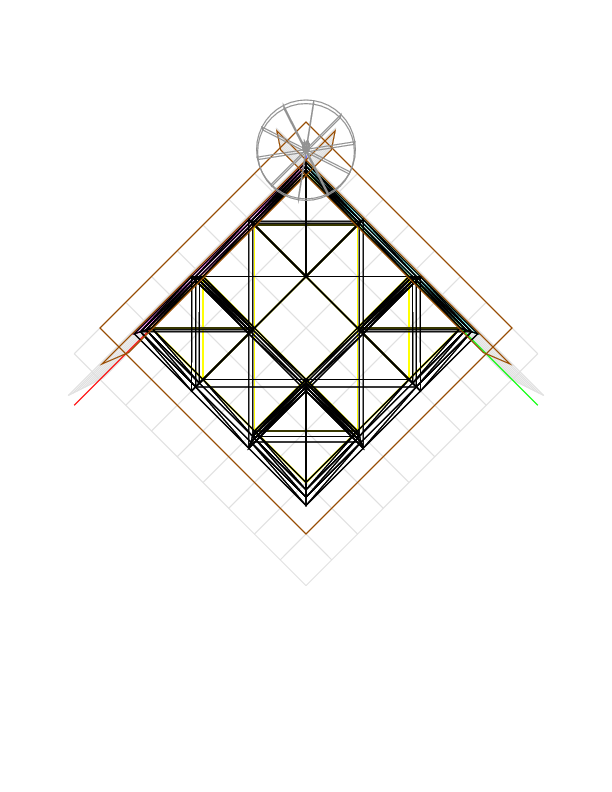
If we cut also in direction (0, -1, 0), the tool can reach through the hole parallel to the y axis. Each hole has volume 6 * (2 * 2 - (4 - pi) * 0.6 * 0.6) =~ 22.1458. The holes meet in the center of the cube. The volume of the intersection is 16 * 0.6 * 0.6 * 0.6 / 3 + (24 - 4 * pi) * 0.4 * 0.6 * 0.6 + 24 * 0.4 * 0.4 * 0.6 + 8 * 0.4 * 0.4 * 0.4 =~ 5.61444. After cutting, the volume remaining is approximately 6 * 6 * 6 - 2 * 22.1458 + 5.61444 =~ 177.323, and the device gives 175.9232.

Hollow cube cut from three directions

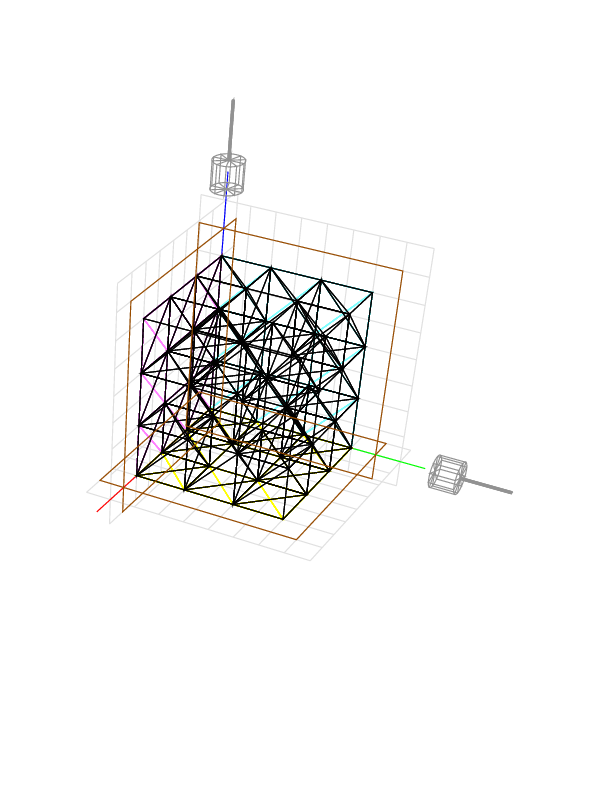
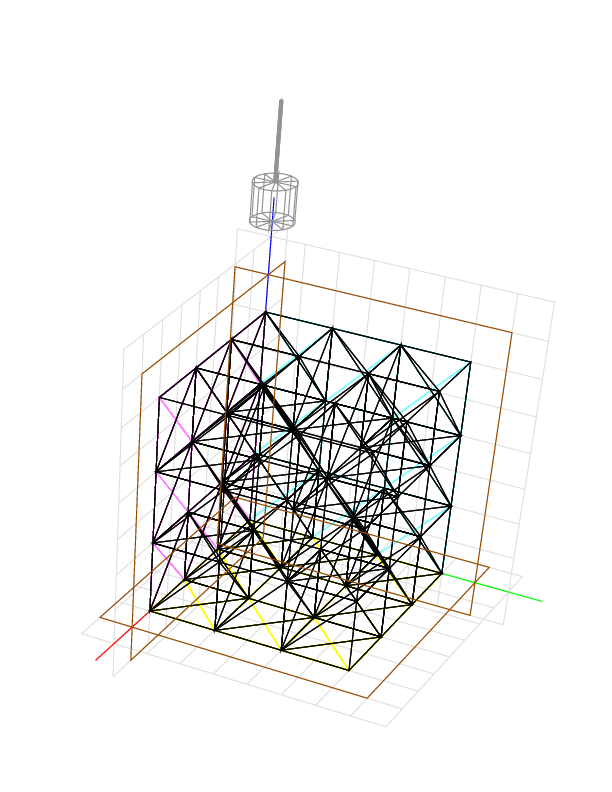
We add one more cutting direction to reach the rest of the material. The device gives 165.2224.

Cup cut from below

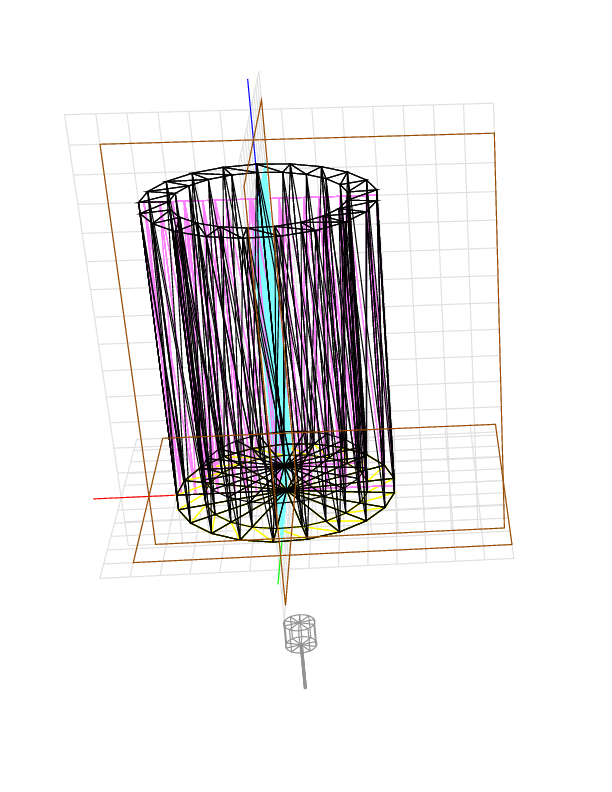
This cup is a polyhedral approximation of a cylindrical cup with outer radius 4 units, inner radius 3, and height 11. The sides and bottom are 1 unit thick. Cutting from below, the tool cannot reach inside the cup. The blank extends 2 units above (and below) the cup top, so the volume remaining is roughly 13 * pi * 4 * 4 =~ 653.451. More precisely, the side of the cup is not really round, but has 21 flat faces. The true volume remaining is 13 * 21 * 4 * sin(pi/21) * 4 * cos(pi/21) =~ 643.745. The device gives 638.43.

Cup cut from above

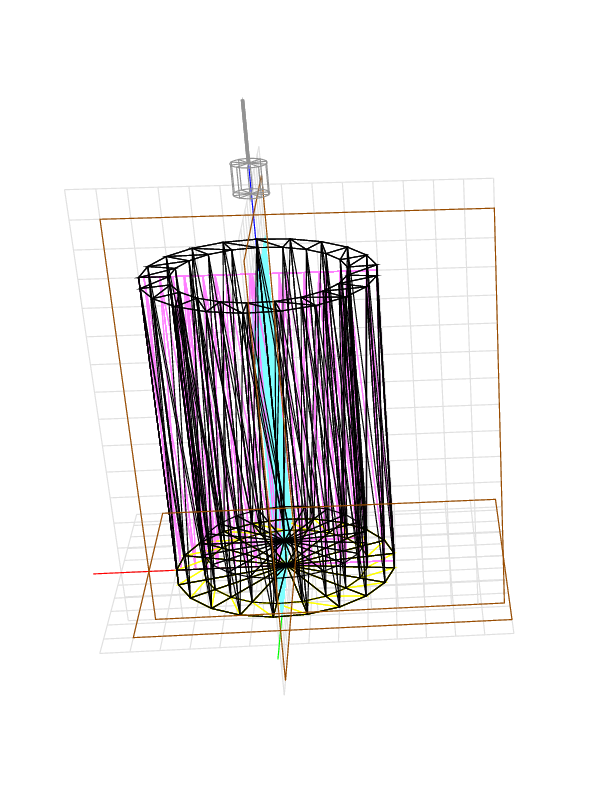
If instead we cut from above, the volume remaining is roughly 13 * pi * 4 * 4 - 10 * pi * 3 * 3 =~ 370.708, or more precisely, 13 * 21 * 4 * sin(pi/21) * 4 * cos(pi/21) - 10 * 21 * 3 * sin(pi/21) * 3 * cos(pi/21) =~ 365.202. The device gives 363.675 .

Cup cut from above and from below

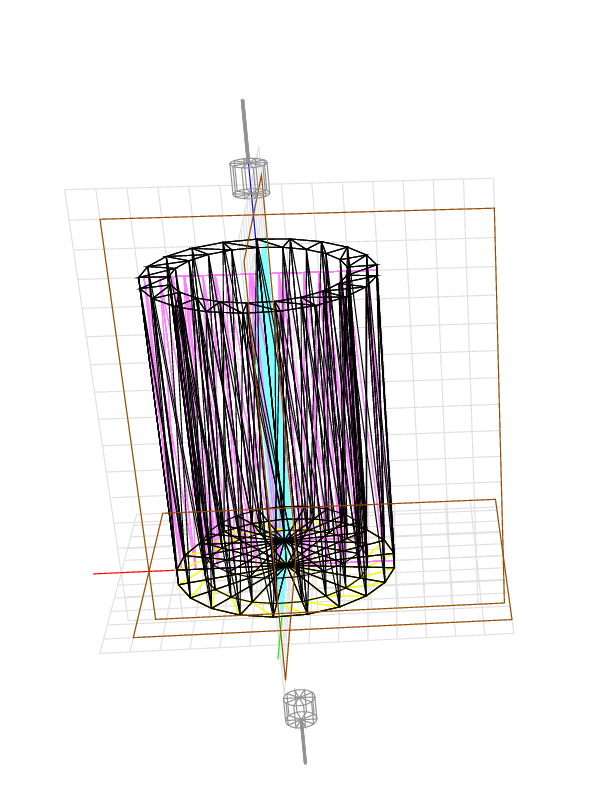
If we cut from both above and below, the volume remaining is roughly 11 * pi * 4 * 4 - 10 * pi * 3 * 3 =~ 270.177, or more precisely, 11 * 21 * 4 * sin(pi/21) * 4 * cos(pi/21) - 10 * 21 * 3 * sin(pi/21) * 3 * cos(pi/21) =~ 266.164. The device gives 278.46. On another day I got 260.52 and 271.83. The device runs on electricity. Right now it is configured to use little power. It will produce more accurate results if we turn up the power.

Mug cut from below

A handle is added to the cup. The device gives 692.64.

Mug cut from above

The device gives 415.74.

Mug cut from above and from below

The device gives 285.675.

Mug cut from three sides

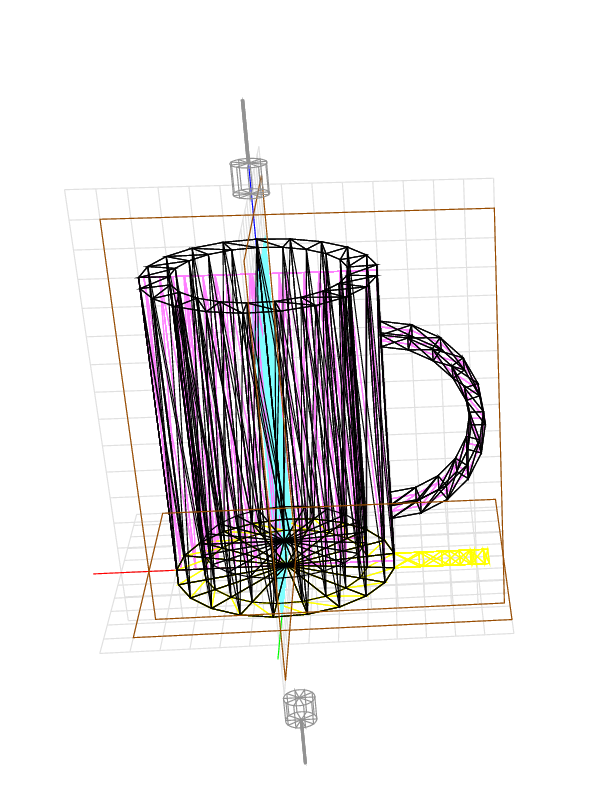
If we cut also in the y direction, we remove most of the material between the handle and the mug. The device gives 269.1.

Input format

1. BitRadius: the radius of the cutting tool
2. RangeX: values x0 and x1, where the initial block from which the designed object is cut is [x0, x1] x [y0, y1] x [z0, z1]. We should verify that the initial block contains the whole object. We might use the bounding box, that is, the smallest block that contains the object, but if the object fills most of its bounding box, the volume estimate will be most accurate if the initial block is roughly twice as large as the object in volume.
3. RangeY: values y0 and y1 as described in section RangeX
4. RangeZ: values z0 and z1 as described in section RangeX
5. CuttingDirections: the directions in which the cutting tool plunges. Each row has three numbers x y z not all 0.
6. Triangles: each row x0 y0 z0 x1 y1 z1 x2 y2 z2 represents a triangular facet with vertices (x0, y0, z0), (x1, y1, z1), and (x2, y2, z2).

Example

  BitRadius:
  0.6
  RangeX:
  -2 8
  RangeY:
  -1 9
  RangeZ:
  -1 10.5
  CuttingDirections:
  1  0    0
  1 -1.2  0
  Triangles:
    0   0   0      1   0   0      1.1 -0.2 6.3  
  -1.2 2.4 4.5    4.4 5.5 6.6     7.7  8.8 9.9  

Conclusion

Thank you for reading this technical note. My aim is to help people in industry with scheduling and estimating costs. No promises, but if you send me a small design, say of at most 5000 triangles and at most 7 cutting directions, I will run the device on your design and send you the result. Please include all the parameters described above. Email me at david.a.c.v.smith@gmail.com with subject VOLUME. If you send an STL file, I will find it easier to read text (ASCII) rather than binary. I can accept .zip files or files compressed in the style of Unix (https://kb.iu.edu/d/aeqx).